1変数$n$次方程式
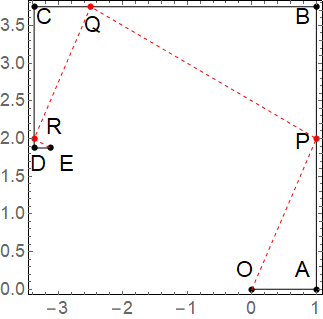
この実数解を得るために、以下のように$xy$座標平面上に点と直線を図示していく。まず、原点Oから出発して、右($x$軸の正方向)に$a$だけ進んだ場所を点A、そこから上($y$軸正方向)に$b$だけ進んだ場所を点Bとする。同様に、点Bから左に$c$進んだ場所を点C、下に$d$進んだ場所を点$D$、右に$e$進んだ場所を点$E$とする。このように、反時計周りに点を選び、それらを直線で結んだ図を作る(Fig. 1参照)

次に、原点Oと点Eを結ぶ"レーザー"(線分)を以下のルールを用いて図示する。まず、点Oから線分AB上(一般にはABを延長した直線)に向けてレーザーを発射し、その直線ABとの交点をPとする。次に、点Pで直線BC上の方向にレーザーが"反射"すると仮定する。ここで、レーザーの反射角$\angle OPQ$は90度を満たすと仮定する。同様に点Qはレーザーが"反射"し、それを繰り返し、最終的にレーザーが点Eを通過するようにする(Fig.2参照)。実はこのように点Oから点Eを通過する線分を作ったとき、点Pの$y$座標に(-1)をかけた値が求めたい方程式の実数解となることを示すことが出来る。
実際、例えば$a=1,b=15/4, c=35/8, d=15/8, e=1/4$のとき、方程式は
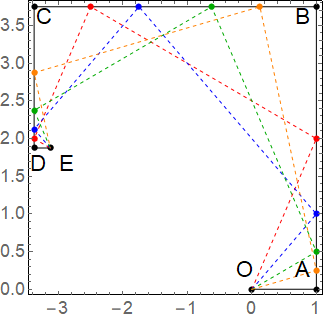
Fig.3 議論した4次方程式の実数解の幾何学解。
このようば方程式の幾何学的解法はLillの方法と呼ばれ、19世紀半ばに発見されたらしい[1,2]。上記では方程式の$x^n$の各係数を正と仮定して説明したが、一般にその仮定は不要であり、各係数が負の場合でも同様の手順で解を得ることができる。
補足:Lillの法則の証明
ここでは、何故この方法で解が得られるのかを説明しよう。わかりやすさのために以下では$n=4$と仮定して説明を行う。 まず、Fig.2において$\triangle OAP$, $\triangle PBQ$, $\triangle QCR$, $\triangle RDE$がすべて相似となる事に注意する。よって、これら三角形の各辺の比が等しくなることから
参考文献
[1] Wikipedia: Lill's method
[2] トーマス・ハル著、羽鳥公士郎訳、ドクター・ハルの折り紙数学教室, 日本評論社 (2015).
\begin{eqnarray} f(x)=a_n x^n+a_{n-1}x^{n-1}+\cdots +a_0=0, \ a_n =1
\end{eqnarray}
の実数解を幾何学的に得る方法を紹介しよう。その方法を以下では$n=4$の場合、すなわち、\begin{eqnarray}
a x^4+ bx^3+cx^3+dx+e=0, \ a =1
\end{eqnarray}に対して説明しよう。この実数解を得るために、以下のように$xy$座標平面上に点と直線を図示していく。まず、原点Oから出発して、右($x$軸の正方向)に$a$だけ進んだ場所を点A、そこから上($y$軸正方向)に$b$だけ進んだ場所を点Bとする。同様に、点Bから左に$c$進んだ場所を点C、下に$d$進んだ場所を点$D$、右に$e$進んだ場所を点$E$とする。このように、反時計周りに点を選び、それらを直線で結んだ図を作る(Fig. 1参照)

Fig.1 $x^4+ bx^3+cx^2+dx+e=0$を解くための図(ここでは説明のために$a=1$,$b=15/4$, $c=35/8$, $d=15/8$, $e=1/4$と仮定した)。
次に、原点Oと点Eを結ぶ"レーザー"(線分)を以下のルールを用いて図示する。まず、点Oから線分AB上(一般にはABを延長した直線)に向けてレーザーを発射し、その直線ABとの交点をPとする。次に、点Pで直線BC上の方向にレーザーが"反射"すると仮定する。ここで、レーザーの反射角$\angle OPQ$は90度を満たすと仮定する。同様に点Qはレーザーが"反射"し、それを繰り返し、最終的にレーザーが点Eを通過するようにする(Fig.2参照)。実はこのように点Oから点Eを通過する線分を作ったとき、点Pの$y$座標に(-1)をかけた値が求めたい方程式の実数解となることを示すことが出来る。

Fig.2 $\angle OPQ=\angle PQR= \angle QRE=90^\circ{}$を満たすように点Oと点Eを通るような線分を図示する。
実際、例えば$a=1,b=15/4, c=35/8, d=15/8, e=1/4$のとき、方程式は
\begin{eqnarray} x^4+ bx^3+cx^2+dx+e=(x+2)(x+1)(x+1/2)(x+1/4) \end{eqnarray}
と因数分解され、解は$x=-1/4, -1/2, -1, -2$となる。これらの解が上記プロセスで得られることはFig.3から確認出来る。
Fig.3 議論した4次方程式の実数解の幾何学解。
このようば方程式の幾何学的解法はLillの方法と呼ばれ、19世紀半ばに発見されたらしい[1,2]。上記では方程式の$x^n$の各係数を正と仮定して説明したが、一般にその仮定は不要であり、各係数が負の場合でも同様の手順で解を得ることができる。
補足:Lillの法則の証明
ここでは、何故この方法で解が得られるのかを説明しよう。わかりやすさのために以下では$n=4$と仮定して説明を行う。 まず、Fig.2において$\triangle OAP$, $\triangle PBQ$, $\triangle QCR$, $\triangle RDE$がすべて相似となる事に注意する。よって、これら三角形の各辺の比が等しくなることから
\begin{eqnarray}
\frac{OA}{AP}=\frac{PB}{BQ}=\frac{QC}{CR}=\frac{RD}{DE}
\end{eqnarray}
が成立する。いま$AP$, $BQ$,$CR$の長さをそれぞれ$p, q, r$と選び、各点$P,Q,R$の座標の作り方を思い出すと、
\begin{eqnarray}
\frac{1}{p}=\frac{b-p}{q}=\frac{c-q}{r}=\frac{d-r}{e}
\end{eqnarray}
が成立する。
この連立方程式は等式が3つあり、未知数が$p,q,r$なので、$q,r$を消去できる。実際に$p$だけの式に書き直すと、$p$は
\begin{eqnarray}
(-p)^4+ b(-p)^3+ c(-p)^2+d(-p)+e=0
\end{eqnarray}
を満たすことを示せる。
したがって、$x=-p$は方程式$x^4+ bx^3+cx^3+dx+e=0$の解となる。参考文献
[1] Wikipedia: Lill's method
[2] トーマス・ハル著、羽鳥公士郎訳、ドクター・ハルの折り紙数学教室, 日本評論社 (2015).
コメント